선형대수학 ( Linear Algebra )
행렬 ( Matrix )
1. 행렬의 기본 [ 중간고사 범위 ]
행렬은 행(Row)과 열(Column)로 이루어졌다.

- 정방행렬 (Square Matrix) : 행의 크기와 열의 크기가 같은 행렬
- 주 대각선 (Main Diagonal) : 정방행렬의 대각선 항
- a11, a22, a33
- 주 대각선 (Main Diagonal) : 정방행렬의 대각선 항
- 행렬간 연산
- 덧셈 & 뺄셈 ( A + B, A - B )
- 같은 위치의 항끼리 연산한다.
- 결과 행렬 M의 성분 Mrc에서, Mrc = Arc (+, -) Brc이다.
- 교환 법칙 → A + B = B + A
- 결합 법칙 → (A + B) + C = A + (B + C)
- 항등 법칙 → A + O = O + A
- 역원 → A + ( -A ) = O
- 곱셈 ( A * B )
- 행렬 A의 열 크기와 행렬 B의 행 크기가 같을 때만 곱셈이 가능하다.
조건 : [ 행렬 A - a * n ] [ 행렬 B - n * b ]
- 결과 행렬 M의 성분 Mrc에서, Mrc = Ar1*B1c + Ar2*B2c +... + Arn*Bnc이다.
- 결합 법칙 → A(BC) = (AB)C
- 분배 법칙 → A(B+C) = AB + AC
- 스칼라 곱 → k(AB) = (kA)B = A(kB)
- 항등식 → IA = A
- 스칼라곱 ( k*A )
- 행렬 A의 모든 성분에 k를 곱한다.- 분배 법칙 → k(A+B) = kA + kB, (c+d)A = cA + dA
- 분배 법칙 → k(A+B) = kA + kB, (c+d)A = cA + dA
- 덧셈 & 뺄셈 ( A + B, A - B )
- 부행렬 ( Submatrix )
- 하나의 큰 행렬을 같은 크기의 여러 작은 행렬로 나눈 것.
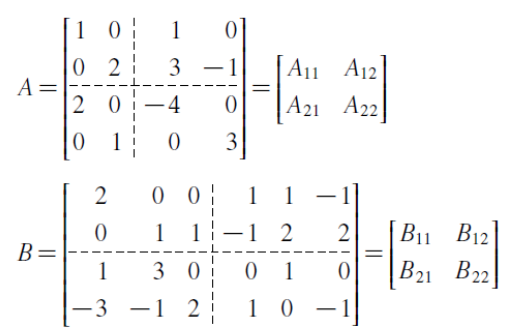
- 행렬의 종류
- 대각 행렬 ( Dignoal Matrix )
- 주 대각선 성분을 제외한 모든 항이 0인 행렬
[ a12, a13, a21, a23, a31, a32 = 0 ]
- 주 대각선 성분이 모두 1인 경우, 단위 행렬 ( Identity Matrix, I )
[ a11, a22, a33 = 1 ]
- 단위 행렬에서 임의의 행의 위치를 교환한 경우, 치환 행렬 ( Permutation Matrix ) - 영 행렬 ( Zero Matrix, O )
- 모든 항이 0인 행렬 - 전치 행렬 ( Transpose Matrix, AT )
- 행렬을 주 대각선을 기준으로 뒤집은 행렬
- 정방행렬이면서 A = AT인 경우, 대칭 행렬 ( Symmetric Matrix )
- 정방행렬이면서 A = -AT인 경우, 교대 행렬 ( Skewed-Symmetric Matrix ) - 삼각 행렬 ( Triangular Matrix )
- 정방행렬이면서 주 대각선을 기준으로 위나 아래의 모든 항이 0인 행렬
- 주 대각선의 위가 모두 0인 경우, 하부삼각 행렬
- 주 대각선의 아래가 모두 0인 경우, 상부삼각 행렬
- 대각 행렬 ( Dignoal Matrix )
- 기본 행 연산 ( Elementary Row Operation )
- 행 동치 ( Row Equivalent ) : 행렬 A의 모든 행을 행렬 B의 행의 선형 결합으로 나타낼 수 있다.
- 피벗 ( Pivot ) : 행렬의 각 행에서 가장 왼쪽에 나타나는 0이 아닌 수
- 행 사다리꼴 ( Row Echelon Form, REF ) : 각 피벗의 아래의 모든 항이 0인 행렬
[ 행 사다리꼴을 구하기 위해, 가우스 소거법을 수행한다. ( 전향단계 ) ]
- 기약 행 사다리꼴 ( Reduced REF ) : 각 피벗의 위 아래 모든 항이 0인 행렬
[ 기약 행 사다리꼴을 구하기 위해, 조단 소거법을 수행한다. ( 우향단계 ) ]
- 계수 ( Rank ) : 행렬의 총 피벗의 개수
- 1. 임의의 행 2개의 위치를 서로 바꾼다.
- 2. 임의의 행에 0이 아닌 상수를 곱한다.
- 3. 임의의 행에 0이 아닌 상수를 곱한 후, 다른 행에 더한다.
- 행렬의 특징
- Det( I ) = 1
- 행렬 내에서 행의 위치를 변경하면 행렬식의 부호가 변경된다.
- 정방행렬 A의 임의의 한 행 또는 열에 스칼라 상수 k를 곱한 후 행렬식을 구하면,
Det( A ) * k와 같다. - 행렬에 같은 행이 2개 존재하면 행렬식이 0이다.
- 기본 행 연산의 수행으로 행렬식이 변하지 않는다.
- 모든 항이 0인 행이 하나라도 존재하면 행렬식은 0이다.
- 삼각행렬의 행렬식은 주 대각선의 곱과 같다.
- Det( A * B ) = Det( A ) * Det( B )
- Det( A ) = Det ( AT )
- 행렬식이 0이 아니면 역행렬이 존재하며, 역도 성립한다.
2. 행렬 계산 [ 중간고사 범위 ]
행렬식(Determinant), 역행렬(Inverse Matrix), LU 분해(LU Decomposition)
- 행렬식 (Determinant, |A|, det(A))
- 2차 행렬식 공식
= ad - bc - 3차 행렬식 공식 (사루스의 공식, Sarrus's Formula)
= ( a11a22a33 + a12a23a31 + a13a21a32 ) - ( a11a23a32 + a12a21a33 + a13a22a31 ) - 여인수를 이용한 3차 행렬식 계산
- 소행렬식 ( Minor ) : 소행렬식 Mij에 대해, A의 i행, j열을 제외한 나머지 원소들의 행렬식
[ M11 = (a22 * a33) - (a23 * a32) ]
- 여인수 ( Cofactor ) : 소행렬식에 +, - 부호를 붙인 것
[ Cij = (-1)i+j * Mij ]
임의의 한 행에 대해, Det(A) = an1*Mn1 + an2*Mn2 + an3*Mn3이다.
- 2차 행렬식 공식
- 역행렬 ( Inverse Matrix )
- 행렬 A와 B가 모두 정방행렬일 때, 'AB = BA = I'인 행렬 B가 존재하는 경우, 행렬 A는 가역적이다.
이 때, 행렬 B를 행렬 A의 역행렬이라고 한다.
- 역행렬의 성질
- Det( A ) = 0이면, A는 특이 행렬이고, 역행렬이 존재하지 않는다.
- Det( A ) != 0 이면, A는 정칙 행렬이고, 역행렬이 존재한다.
- 역행렬은 여러 개 존재할 수 없다.
- (A-1)-1 = A
- (A*B)-1 = B-1 * A-1
- A * A-1 = I
- (A-1)T = (AT)-1 - 역행렬을 구하는 방법
- 방법 1. 역행렬을 변수로 놓고, 서로 곱해 항등 행렬이되도록 한다.
- 방법 2. 첨가행렬 (Argumented Matrix)에 기본 행 연산을 수행한다.
- 방법 3. 수반행렬 (Adjugate Matrix, Adj)를 통해 구한다.
- 수반 행렬 : A의 여인수를 성분으로 갖는 행렬의 전치행렬
A-1 = ( 1 / det( A ) ) * Adj(A)
- 역행렬의 성질
- 선형방정식의 해 구하기
- 행렬 A가 가역적이고, Ax = b가 n개의 변수와 n개의 방정식을 가지면 유일한 해를 갖는다.
- 크래머의 규칙 ( Cramer's Rule )
- 가역적인 행렬 A, 1*n 크기의 행렬 b에서, Ax = b를 만족하는 해집합 x의 크기는 1*n이다.
xn = det( Bn ) / det( A )
- A의 행렬식을 이용해 A의 역행렬을 구하며, 대수적으로 깔끔하게 정리된다.
- 그러나, 행렬의 크기가 커질수록 계산의 수가 많아져서 비효율적이다. - 첨가 행렬을 이용해 풀이 ( 후방대입법, Back Substitution )
- Ax = b에서 첨가행렬 [ A | b ]를 만든 후, 기본 행 연산을 수행하여 A를 삼각행렬로 만든다.
이후, 역대입법을 통해 해를 구한다.
- 삼각행렬 꼴에서 피벗이 존재하지 않는 행이 있다면, 행이 존재하지 않는다.
- 크래머의 규칙 ( Cramer's Rule )
- LU 분해 ( LU Decomposition )
- 행렬 A를 하부삼각행렬(L)과 상부삼각행렬(U)의 곱으로 분해하는 것이다.
- 행렬 A를 상부삼각행렬로 만들기 위해 곱해야 하는 소거행렬(Elimination Matrix)을 구하고,
양변에 소거행렬 E의 역행렬을 곱해 분해를 완료한다.
- 행렬 A의 소거 과정에서, i번째 행에 k를 곱해서 j번째 행에서 더하는 기본 행 연산에 대해,
단위 행렬에 aij = -k를 추가하면, 해당 기본 행연산을 수행하는 소거행렬이 된다.
※ 이 소거행렬의 역행렬은 aij의 부호를 뒤집으면 된다.
- 행렬 A의 소거 과정에서, i번째 행과 j번째 행을 바꾸는 기본 행 연산에 대해,
단위 행렬의 i번째 행과 j번째 행을 교환하면, 해당 기본 행연산을 수행하는 치환행렬이 된다.
※ 이 치환행렬의 역행렬은 전치로 구할 수 있다.
- LDU Decomposition
- 행렬 L, U의 대각 성분을 모두 1로 만들기 위해, 대각행렬 D를 추가한다.
- 행렬 D는 U의 대각 성분들의 카피다.
- 행렬 U는 각 행에 대해 '(row n) / pivot of row n'의 결과 행이 된다.
- LDU Decomposition
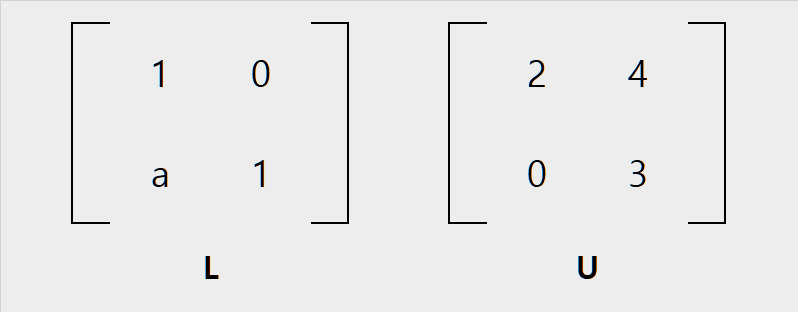
U 행렬에 대해 LDU분해를 진행하면
D의 대각 성분은 2, 3이 되고
U의 첫번째 행은 '[2 4] / 2 = [1 2]'
U의 두번째 행은 '[0 3] / 3 = [0 1]'이 된다.
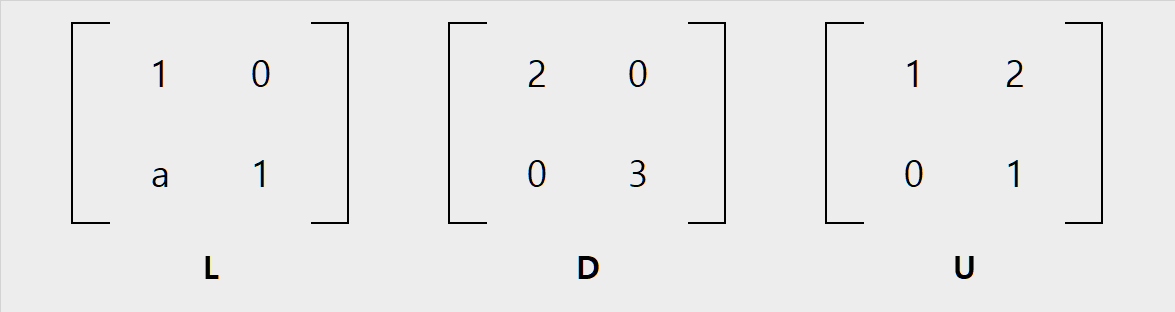
검산
벡터 ( Vector )
1. 벡터와 벡터공간 [ 기말고사 범위 ]
(압력, 속력, 체적, 지름 등) 물리적 양을 실수 크기로 나타낸 정보를 '스칼라'
(속도, 힘, 가속도 등) 크기와 방향을 포함하는 정보를 '벡터'라고 한다.
- 벡터는 시점(Initial Point)에서 종점(Terminal Point)로 가는 유향선분(Directed Segment)다.
- 원점을 시점으로 갖는 벡터는 위치벡터(Position Vector)다.
- 벡터의 시점과 종점을 무시하고 크기의 방향만을 고려하는 벡터는 기하벡터(Geometric Vector)다.
- 벡터 v1, v2를 기하벡터로 볼 때 같다면, 두 벡터 v1, v2는 동치(Equivalent)다.
- 벡터 v의 크기는 Magnitude라고 하며, || v ||로 표기한다.
- Magnitude가 1인 벡터를 단위벡터(Unit Vector, e)라고 한다.
벡터 v와 같은 방향을 가리키는 단위벡터를 구하는 식 $$ \frac {1} {||v||} * v$$
- 기저 벡터 ( Basis Vector, Unit Coordinate Vector)
$$
\mathbf {v_x} = \left[ \begin{array}{r} 1\\0\\0 \end{array} \right] \mathbf {v_y} = \left[ \begin{array}{r} 0\\1\\0 \end{array} \right] \mathbf {v_z} = \left[ \begin{array}{r} 0\\0\\1 \end{array} \right]
$$
- 벡터의 연산
- 벡터의 합차 : 대응하는 각 성분끼리 서로 더한다.
$$
\mathbf {v} = \left[ \begin{array}{r} v_x \\ v_y \end{array} \right] \mathbf {w} = \left[ \begin{array}{r} w_x \\ w_y \end{array} \right] \mathbf {v + w} = \left[ \begin{array}{r} v_x + w_x \\ v_y + w_y \end{array} \right]
$$
- 벡터의 스칼라곱 : 모든 항에 스칼라 값을 곱한다.
$$
\mathbf {v} = \left[ \begin{array}{r} v_x \\ v_y \end{array} \right] \mathbf {kv} = \left[ \begin{array}{r} kv_x \\ kv_y \end{array} \right]
$$
- 벡터의 연산
- 벡터공간 ( Vector Space )
- 다수의 벡터가 모여 형성한 하나의 공간으로, 한 공간 상의 벡터들 사이의 연산의 결과는 그 공간에 존재한다.
이 때, 연산 결과 벡터가 그 공간을 벗어난다면 해당 공간은 닫혀있지 않다.
- 벡터공간은 실벡터공간(Real Vector Space)과 복소 벡터공간(Complex Vector Spaces)로 나뉜다.
- 부분공간 ( Subspace )
- 임의의 N차원 공간에 포함되면서, N차원 벡터들에 대해 선형성을 띄는 작은 공간
2차원 공간의 부분공간 : 영벡터, 원점을 포함한 선, 공간 전체
3차원 공간의 부분공간 : 영벡터, 원점을 포함한 선, 원점을 포함한 면, 공간 전체 - 행렬의 부분공간
- 각 열의 벡터와 그 벡터로 만들 수 있는 모든 선형결합 벡터의 범위
- N차원 행렬의 부분공간은 (N-1)차원 모양의 공간이 나온다.
- 열 공간 ( Column Space )
- 행렬 A의 열들의 선형결합으로 만들어진 부분 공간으로, C(A)로 표기한다.
그러나, A의 열행렬 만으로는 열 공간 전체를 채울 수 없다. - 영 공간 ( Null Space )
- 선형방적식 Ax=O를 만족하는 해집합으로, N(A)로 표기한다.
- 모든 영 공간에는 영 벡터가 포함된다.
- Ax=O의 해를 구하기 위해 소거를 진행하는 과정에서, 영 공간은 변하지 않는다.
이 때, 소거가 완료된 행렬 U에 대해 임의의 열의 피벗이 0이면 왼쪽 열에 종속적이며,
Ax=O와 Ux=O의 해는 같은 영 공간에 존재한다.
- 열 공간 ( Column Space )
- Ux=O의 해를 구하는 방법
- 피벗이 존재하는 열은 Pivot Column, 존재하지 않는 열은 Free Column
- Free Column에 대응하는 x 행렬의 항에는 0,1 을 임의로 설정할 수 있다.
이 때, 임의의 Free Variable를 설정하여 구한 해가 Special Solution이다.
※ Special Solution의 수 = Column count - rank - Ax=b의 완전 해(Complete Solution)를 구하는 방법
- 1. 행렬 A의 가해조건을 확인한다. [ 해가 존재하는가? ]
좌변에 대한 선형 결합이 0을 만들면, 우변에 대한 동일한 선형 결합이 0을 만든다.
※ 행렬 A에 대해 row1+row2-row3=0 면, 행렬 b에 대해 b1+b2-b3=0
- 2. Particular Soution을 구한다.
Ux=b에서, 모든 Free variable를 0으로 설정한 뒤 다시 계산한 해 x이다.
- 3. Nullspace Solution을 구한다.
Ux=0의 특수해들의 선형 결합의 결과가 x_n이다.
- 4. 완전해 x는 x_p + x_n이다.
영공간은 원점을 지나는 부분공간이지만, x_p가 더해지면서 shift된다. - 벡터 행렬의 성질
- m * n 행렬의 계수 r에 대해,
- r = m = n이면, Ax=b에 대해 오직 하나의 해만 존재한다.
- r = n < m 이면, 해가 없거나 하나의 해만 존재한다.
- r = m < n 이면, 무한대의 해가 존재한다.
- r < m, r < n 이면, 해가 없거나 무한대의 해가 존재한다.
- Ax=b (계수행렬 A, 상수행렬 B)와 미지수의 수 c에 대해,
- rank( A ) = rank( A | b ) = c 이면, 유일한 해를 갖는다.
- rank( A ) = rank( A | b ) != c 이면, 무한대의 해를 갖는다.
- rank( A ) != rank ( A | b ) 이면, 해가 존재하지 않는다.
- 임의의 여러 벡터에 대해, 모든 계수가 0인 경우를 제외하는 어떠한 선형 조합으로도 0을 만들 수 없으면
해당 벡터들은 서로 독립이다. 0을 만들 수 있다면 종속이다.
이 때, 종속인 벡터들은 같은 방향을 가리키므로, 좌표 상에서 직관으로 구분이 가능하다.
- 부분공간 ( Subspace )
[ Ax=b의 완전 해 구하기 ]
1. 선형방정식을 [A | b]의 첨가행렬 형태로 만든다.
$$ \begin {array} {r} x_1 + 2x_2 + 2x_3 + 2x_4 = b_1 \\ 2x_1 + 4x_2 + 6x_3 + 8x_4 = b_2 \\ 3x_1 + 6x_2 + 8x_3 + 10x_4 = b_3 \end {array} \longrightarrow \left[ \begin {array} {cccc|c} 1 & 2 & 2 & 2 & b_1 \\ 2 & 4 & 6 & 8 & b_2 \\ 3 & 6 & 8 & 10 & b_3 \end {array} \right] $$
2. 행렬을 소거하여 A를 U형태로 만든다.
$$ \left[ \begin {array} {cccc|c} 1 & 2 & 2 & 2 & b_1 \\ 2 & 4 & 6 & 8 & b_2 \\ 3 & 6 & 8 & 10 & b_3 \end {array} \right] \longrightarrow \left[ \begin {array} {cccc|c} 1 & 2 & 2 & 2 & b_1 \\ 0 & 0 & 2 & 4 & b_2 - 2b_1 \\ 0 & 0 & 0 & 0 & b_3 - b_2 - b_1 \end {array} \right] $$
3. U가 가해조건을 만족하는가를 검사한다.
rank( U ) = 2, rank( U | b ) = 2, 미지수의 수 = 4 이므로,
무한대의 해를 갖는다.
4. Particular Solution을 구한다. ( 행렬 U에서 free columns는 2열, 4열이다 )
$$ \mathbf {x} = \left[ \begin {array} {c} x_1 \\ 0 \\ x_3 \\ 0 \end {array} \right] \longrightarrow \begin {array} {c} x_1 + 2x_3 = 1 \\ 2x_3 = 3 \end {array} \longrightarrow x_1 = -2, x_3 = \frac {3} {2} \longrightarrow \mathbf {x_p} = \left[ \begin{array}{c} -2 \\ 0 \\ \frac {3} {2} \\ 0 \end{array} \right] $$
5. Nullspace Solution을 구한다.
$$ \mathbf {s_2} \Rightarrow \left[ x_2 = 1, x_4 = 0 \right] \Rightarrow \left[ \begin {array} {c} -2 \\ 1 \\ 0 \\ 0 \end {array} \right] , \mathbf {s_4} \Rightarrow \left[ x_2 = 0, x_4 = 1 \right] \Rightarrow \left[ \begin {array} {c} 2 \\ 0 \\ -2 \\ 1 \end {array} \right] \\ \mathbf {x_n} = \mathbf {c_1} \left[ \begin {array} {c} -2 \\ 1 \\ 0 \\ 0 \end {array} \right] + \mathbf {c_2} \left[ \begin {array} {c} 2 \\ 0 \\ -2 \\ 1 \end {array} \right] $$
6. x_p와 x_n을 더해 Complete Solution을 구한다.
$$ \mathbf {x} = \mathbf{x_p} + \mathbf{x_n} \Rightarrow \mathbf{x} = \left[ \begin{array}{c} -2 \\ 0 \\ \frac {3} {2} \\ 0 \end{array} \right] + \mathbf {c_1} \left[ \begin {array} {c} -2 \\ 1 \\ 0 \\ 0 \end {array} \right] + \mathbf {c_2} \left[ \begin {array} {c} 2 \\ 0 \\ -2 \\ 1 \end {array} \right] $$
2. 고유공간 ( Eigenspace )
고유값과 고유벡터는 정방행렬에 대해서만 정의된다.
- 생성(Span), 기저(Basis), 차원(Dimension)
- 두 개 이상의 벡터가 선형 조합을 통해 공간을 만드는 것을 생성(Span)이라고 한다.
행렬 A의 열 공간 C(A)는 A의 열벡터들이 Span한 공간이다.
이 때, 공간을 Span하는 서로 독립인 벡터를 기저 벡터(Basis Vector)라고 하며,
공간의 각 축을 대표하는 기저의 형태를 표준 기저(Standard Basis)라고 한다.
한 공간에 대한 모든 기저는 같은 수의 벡터를 가지며, 이 벡터의 수가 차원(Dimension)의 크기를 나타낸다.
행렬 U에서 Pivot Column이 기저가 된다.
- 고유값(Eigenvalue), 고유벡터(Eigenvector), 고유공간(Eigenspace)
- 행렬 A * 벡터 x의 결과 벡터 Ax가 x와 같은 방향을 가리킬 때, Ax는 고유벡터(Eigenvector)다.
이 때 두 벡터가 평행하므로 Ax = λx로 정의할 수 있고, 여기서 특정한 상수 λ는 고유값(Eigenvalue)다.
한 벡터 x에 대해, 고유값은 유일하고, 고유벡터는 무수히 많다.
- 고유값의 성질
- 행렬 A의 모든 λ에 대해, λ1 + λ2 + ... + λn = trace(A)
- 행렬 A의 모든 λ에 대해, λ1 * λ2 * ... * λn = det(A)
- AT 와 A의 고유값은 같다.
- A-1의 고유값은 1/λ1, 1/λ2, ..., 1/λn 이다.
- 스칼라 k에 대해, kA의 고유값은 kλ1, kλ2, ..., kλn 이다.
- 치환 행렬에 kI를 더한 행렬에서, 고유값은 k만큼 더해지고 고유벡터는 변하지 않는다. - 고유공간 ( Eigenspace )
- 행렬 A의 고유벡터들이 형성하는 부분공간이 고유공간(Eigenspace)이다.
일반적으로, 고유공간은 선(Line)의 형태를 띈다. ( 모든 벡터가 한 방향을 가리키므로 )
- 행렬 A의 고유값이 0이면 Ax=0이고, 따라서 고유벡터는 Nullspace에 존재한다.
이 때, Nullspace가 존재하기 위해서는 free variable이 존재해야한다.
그리고 free Variable이 존재하기 위해서는 A가 특이행렬이여야한다. - 고유값 구하기
$$ \mathbf { Ax } = \mathbf { \lambda x } \Rightarrow \mathbf { Ax } - \mathbf { \lambda x } = 0 \Rightarrow \left( \mathbf { A } - \mathbf { \lambda I } \right) \mathbf {x} = 0 \\ \left( \mathbf { A } - \mathbf { \lambda I } \right) = \begin{bmatrix} a & b \\ c & d \end{bmatrix} - \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \end{bmatrix} = \begin{bmatrix} a - \lambda & b \\ c & d - \lambda \end{bmatrix} \\ \mathbf { det } \left( \mathbf { A } - \mathbf { \lambda I } \right) = \mathbf {0} \qquad \because \mathbf {A} \scriptstyle\text{ is singular matrix} \\ \mathbf { det } \left( \mathbf { A } - \mathbf { \lambda I } \right) = \left( \mathbf {a} - \mathbf {\lambda} \right) \left( \mathbf {d} - \mathbf {\lambda} \right) - \mathbf{bc} = \mathbf{\lambda ^2} - \left( \mathbf {a} + \mathbf {d} \right) \mathbf{\lambda} + \left( \mathbf{ad} - \mathbf{bc} \right) \\ \mathbf{\lambda} = \mathbf{x_1} , \mathbf{x_2}$$ - 고유벡터 구하기
- 위에서 구한 (A-λI) 행렬을 소각하여 삼각행렬로 만들고, 이를 U(λ)라고 한다.
- U(λ)x=0에, 위에서 구한 고유값을 대입하여 식을 푼다.
이 때, x에 들어가는 벡터의 값이 달라져도 결과에 영향을 미치지 않는다.
※고유값을 구할 때, 기본 행 연산을 가한 행렬에서 새로 고유값을 구하면 결과가 달라진다. - 투영행렬을 이용한 예시
$$ \mathbf {Ax} = \mathbf{b} \Rightarrow \begin{bmatrix} -3 & 2 \\ -1 & 4 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix} \text {에서} \mathbf {b} \not\in \mathbf {A} \text{'s column space } \left( \mathbf {R^2} \right) \\ \therefore \mathbf {p} = \mathbf {Pb} \qquad \mathbf {P} \text{ is projection matrix, } \left( = A \left( A^{T} A \right)^{-1} A^{T}\right) , \text {p} \in \mathbf {A} \text{'s column space } \\ \\ \text{rank}\left(\mathbf{P}\right) = 2, \mathbf{P} \text{ is singular matrix } , \mathbf{a_n}=\mathbf{Pa_n} \\ \therefore \text{eigenvalues and eigenvectors of Projection Matrix since } \mathbf{Px} = \mathbf{\lambda x} \\\text{, Any vectors x in C(A) : } \mathbf{Px} = mathbf{x} \Rightarrow \mathbf{\lambda} = 1 $$
- 고유값의 성질
- 기타 행렬
- 직교행렬 ( Orthogonal Matrix )
- 행렬의 모든 열 벡터의 크기가 1이며, 각 벡터가 직교한다. - 회전행렬 ( Rotation Matrix )
- 어떤 행렬에 곱했을 때, 크기의 변환 없이 회전에만 관여하는 행렬
- 회전 각도 θ = 0, θ = 180일 때 고유벡터가 실수 범위에 존재하며,
그 외의 회전 각도에 대해 고유벡터는 복소수 범위에 존재한다.
- 이는, 행렬이 대칭형태에 가까울 수록 고유벡터가 실수 범위에,
비대칭 형태에 가까울 수록 복소수 범위에 나옴을 보여준다.
※ 비-대칭 행렬 : AT = -A인 행렬
$$ \mathbf {R} = \begin{bmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \qquad \text{일반적인 2차원 평면 회전 행렬의 형태} $$ - 닮은행렬
- 같은 크기의 정방행렬 A, B, C에 대해, 'B=C^-1 * AC'를 만족하면
A와 B가 서로 닮은 행렬이라고 하며, A, B의 고유값은 같다. - 삼각행렬의 성질
- 삼각 행렬의 각 대각 성분이 고유값이고,
만약 이 대각 성분이 같으면, 같은만큼 구할 수 있는 고유벡터의 수가 줄어든다.
- 직교행렬 ( Orthogonal Matrix )
'3-1공부 > 선형대수학' 카테고리의 다른 글
| 기말3. 기저, 고유값, 고유벡터 (0) | 2022.05.21 |
|---|---|
| 기말2. 벡터 공간 (0) | 2022.05.06 |
| 기말1. 벡터 (0) | 2022.05.06 |
| 5. LU 분해 (0) | 2022.04.17 |
| 4. 선형방정식의 해법 (0) | 2022.04.17 |