· 내용 정리
영상 인식이란, 데이터의 특징을 통해 학습하여 새로운 데이터를 분류하는 과정이다.
주성분 분석(PCA, Principal Component Analysis)을 기반으로 얼굴 인식을 진행해보자.
PCA는 고차원 데이터를 저차원 데이터로 투영하여 사용하는 것인데, 이를 위해 분산이 큰 축을 주 축으로 정의하여 투영한다. 이 때, M차원 공간에 존재하는 모든 벡터는 M 개의 기저벡터의 합으로 표현되며, 이 벡터를 주 축이 될 기저 벡터 e_j에 투영할 경우, 투영된 벡터의 값은 벡터의 전치행렬에 주 축 기저벡터를 곱한 값이 된다.
이 때, 주 축을 찾기 위해 각 차원에 대한 공분산 행렬(Convariance Matrix)를 만들고, 이 행렬을 이용하여 분산이 가장 높은 축을 찾을 수 있다. 주 축을 이용해 고유값과 고유벡터(eigen-value, eigen-vector)를 구할 수 있는데, 얼굴 인식에서는 고유 벡터를 고유 얼굴(eigen face)라고 부르기도 한다. 근데 이제 뒤쪽의 벡터일수록 특징값보다 노이즈가 크므로, 특징값을 나타내는 적절한 경계 N을 찾아, N개의 고유 얼굴만 사용한다.
얼굴 인식을 위해, 학습 영상은 N*M개 화소크기의 2차원 얼굴 영상 P개로 구성되며, 이 때 얼굴 인식 과정은
[1. 학습 영상에서 평균 얼굴을 제거]
[2. 공분산 행렬의 고유 벡터 계산]
[3. 고유값이 큰 고유 벡터 선정]
[4. 1의 결과를 고유 벡터를 이용해 투영]
[5. 결과값의 유사도를 통한 인식]
으로 진행된다.
분류화(Classification)란, 어떤 특징값 공간에서 판단 기준에 따라 몇 개의 Class 중 하나로 분류하는 과정이다. 최종적으로 잘못된 분류를 최소화하는 것이 목표이다.
분류화 작업을 수행하기 위해 인공 신경망(ANN, Artificial Neural Network)을 사용할 수 있다. ANN은 인간의 뇌 구조를 모방한 것으로, 입력 벡터(P)와 가중치 벡터(W)의 내적을 합산 후, 단조증가하는 함수에 입력하는 형태를 가진다. 이 때, 인공 신경망의 성능을 향상시키기 위해, 입력층과 출력층 사이의 신경망 수를 늘리거나(은닉층), 출력 값을 이용한 역전파(Back-propagation)등을 이용할 수 있다. 이 때, Convolution과 Pooling등을 적용하면 2차원 영상의 특징을 분류하는 CNN(Convolutional Neural Network)구조를 만들 수 있다.
또다른 방법은 SVM(Support Vector Machine)이 있다. 추출된 특징값을 바탕으로 분류를 위한 직선 형태의 경계를 만드는 것인데, 분류를 위한 경계(결정 경계)와 가장 가까운 점(서포트 벡터)의 거리(마진)를 최대화하는 것이 특징이다.
분류 성능 평가는 '모델이 입력을 무엇으로 분류하였는가?'에 따라 Positive, Negative가 나눠지며, '모델이 분류한 결과가 정답인가?'에 따라 True, False로 나눠진다. 그리고 이 두 개의 기준에 따라 TP, FP, FN, TN의 4개의 결과로 나눠진다.
이 때, Recall(재현율, Sensitivity, Hit-Rate)은 실제 정답을 정답으로 잘 분류한 비율이며, TP / (TP+FN)으로 나타난다.
Precision(정밀도)는 정답으로 분류한 것 중 실제 정답인 것의 비율이며, TP / (TP + FP)로 나타난다.
Specificity(특이도)는 오답을 오답으로 분류한 확률로 TN / (TN + FP)로 나타낸다.
임의의 점 P의 3차원 공간 상 움직임을 회전 벡터 R과 이동 및 변환 벡터 T를 이용해 표현할 수 있다. 이를 이용해 동영상에서의 움직임을 추정할 수 있으며, 이를 위해 특징 추출 및 영상 정합을 수행할 수 있다.
이 때, 움직임 탐지를 위한 영상 정합 알고리즘은 아래 5가지가 있다.
| 전역 움직임 | 영상 전체를 하나의 움직임 모델로 가정하는 방식으로, 카메라의 이동만 고려한다. |
| 화소 기반 움직임 | 점, 선분 등의 특징점에서 움직임을 추정하는 방식이다. |
| 물체 기반 움직임 | 사전에 물체를 분할하고, 영상에서 이 물체들을 통해 움직임을 추정하는 방식이다. |
| 옵티컬 플로 기반 움직임 | 움직임 전후의 밝기값 변화가 없음을 가정하고, 움직임에 관련된 시각적 자극의 표현을 탐지한다. |
| 블록 기반 움직임 | 영상을 일정 단위 블록으로 구분하여, 블록 단위의 움직임을 추정한다. |
FRUC(Frame Rate-Up Conversion)란, 영상 시간 해상도 개선 기술로, 이미 존재하는 프레임을 없애거나, 시간적으로 연속된 프레임을 참조하여 중간 프레임을 보간하거나 생성하는 방식으로 프레임 속도를 변경한다.
이 때, 영상 내 객체의 움직임을 고려하지 않는 경우, 필터링을 통해 보간 프레임을 생성하여 복잡도는 낮지만, 객체 영역의 블러링이나 모션 저키니스가 발생할 수 있다. 반면, 움직임을 고려하는 경우, 움직임 벡터 기반으로 보간 프레임을 생성하므로 이러한 문제는 없으나 복잡도가 높아진다.
※ 모션 저키니스(Motion Jerkiness)란, 동작의 부드러움, 연속성 등이 결여된 상태이다
<영상 압축, Image Coding>
영상 압축이란, 영상의 통신을 위한 과정으로, 소스 인코더를 통해 영상의 불필요한 데이터를 제거해 압축하고, 채널 인코더에서 데이터 전송을 위해 이진화하는 과정이다. 기본적으로 예측-변환-양자화-엔트로피 코딩 순으로 진행된다.
[1. 예측]
많은 시/공간 평면 예측기를 설계하고, 신호에 따라 선택적으로 사용하여 좋은 예측 신호를 만들 수 있다. 이 때, 대표적인 공간 평면 예측기로는 4x4, 8x8등의 블록 단위로 화소 밝기값을 예측하는 방식이 있다. 이 때, 코덱에 따라 다양한 방식이 있다. 시간 평면 예측기로는 이전 시간에 이미 압축된 영상 정보를 사용하는 방식이 있다.
| I 프레임 | 공간 평면 예측만을 사용하여 부호화된, 자체적으로 완전한 정보를 가진 프레임이다. |
| P 프레임 | 이전 I프레임이나 P프레임을 참조하여 예측된 이미지 정보를 가진 프레임이다. 모션 벡터를 이용해 이전 프레임과의 차이만을 인코딩하여 압축하므로, I프레임에 비해 훨씬 적은 양의 데이터를 가진다. |
| B 프레임 | 이전이나 다음 I프레임, P프레임을 모두 참조하여 예측된 이미지 정보를 가진 프레임이다. 최대한의 암축을 달성하여 가장 적은 데이터를 차지하지만, 과거 미래 프레임 정보가 모두 있어야 디코딩 가능하다. |
<MPEG(Motion Picture Experts Group) 표준의 시간 평면 예측기>
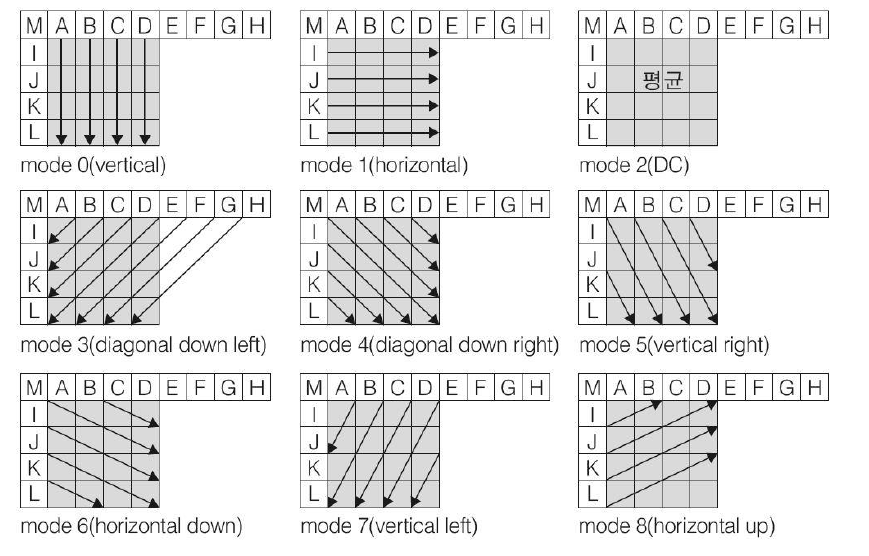
[2. 변환]
N차원 신호들을 적은 축으로 에너지가 몰리도록 하는 직교 변화 기술을 사용한다. 영상 압축 분야에서는 DCT와 같이 고정된 축을 사용하며, 4x4~32x32 등 블록 단위로 DCT와 유사한 정수 변환을 사용하기도 한다.
[3. 양자화]
변환된 계수 값을 몇 개의 구간으로 분할하고, 각 구간을 하나의 정수 값으로 표현한다. 양자화는 비선형적이므로 정보의 손실이 일어나는데, 변환 계수 값을 양자화 한 후 복원하면, 원본과 유사한 블록 값을 복원할 수 있다.
[4. 엔트로피 코딩]
양자화 계수, 예측 모드, 블록 크기 등의 심볼에 최소한의 비트를 할당하여 비트열을 만든다. 이 때, Shannon의 정보 이론에 따르면, 한 심볼의 발생 확률이 P일 때, 이것의 정보량은 log_2(1/P)가 된다. 비트열을 만드는 방식은 허프먼 코딩과 산술 부호화 코딩 등이 있다.
- 허프먼 코딩(Huffman Coding)
각 심볼의 확률에 따라 트리를 구성한 후, 트리 순서대로 코드를 찾는다.
- 산술 부호화 코딩(Arithmetic Coding)
각 심볼의 발생확률에 따라 0에서 1까지의 확률 구간을 분할하여 표현하고자 하는 심볼을 해당 구간의 값 하나로 표현한다.
자주 나오는 심볼은 짧은 비트열, 드물게 나오는 심볼은 긴 비트열을 가진다. 또한, 입력 데이터의 확률 분포에 딱 맞는 코드를 생성하지 못하므로, 최적이 아닌 근사적으로 최적인 코드를 생성하게 된다.
'4-1공부 > DIP' 카테고리의 다른 글
| [기말고사] 11-12장. 영상 형태학, 영상 정합 (0) | 2023.06.16 |
|---|---|
| [기말고사] 8-9장. 영상 기하학, 특징 추출 (0) | 2023.06.13 |
| [중간고사] 6장. 영상 개선 (0) | 2023.04.13 |
| [중간고사] 5장 - 이미지 변환 (0) | 2023.03.31 |
| [중간고사] 4장 - 양자화 (Quantization) (0) | 2023.03.31 |